Perbedaan penting antara geometri Euclidean dan non-Euclidean adalah sifat paralel baris. Euclid ‘s kelima mendalilkan, yang paralel mendalilkan , setara dengan yang Playfair postulat yang menyatakan bahwa, dalam bidang dua dimensi, untuk setiap garis yang diketahui ℓ dan A titik, yang tidak pada ℓ, ada tepat satu garis melalui A yang tidak berpotongan ℓ. Dalam geometri hiperbolik, sebaliknya, ada tak terhingga banyak baris melalui A ℓ tidak berpotongan, sementara dalam geometri eliptik, setiap baris melalui A memotong ℓ (lihat entri pada geometri hiperbolik , geometri berbentuk bulat panjang , dan geometri mutlak untuk informasi lebih lanjut).
Cara lain untuk menggambarkan perbedaan antara geometri adalah mempertimbangkan dua garis lurus tanpa batas waktu diperpanjang dalam bidang dua dimensi yang baik tegak lurus ke saluran ketiga:
- Dalam geometri Euclidean garis tetap konstan jarak dari satu sama lain bahkan jika diperpanjang hingga tak terbatas, dan dikenal sebagai paralel.
- Dalam geometri hiperbolik mereka “kurva pergi” satu sama lain, peningkatan jarak sebagai salah satu bergerak lebih jauh dari titik persimpangan dengan tegak lurus umum, garis-garis ini sering disebut ultraparallels.
- Dalam geometri berbentuk bulat panjang garis “kurva ke arah” satu sama lain dan akhirnya berpotongan.
Sejarah
Sejarah awal
Sementara geometri Euclidean , dinamai matematikawan Yunani Euclid , termasuk beberapa dari matematika tertua, non-Euclidean geometri tidak secara luas diterima sebagai sah sampai abad ke-19.
Perdebatan yang akhirnya menyebabkan penemuan non-Euclidean geometri mulai segera setelah karya Euclid ‘s Elemen ditulis. Dalam Elemen, Euclid dimulai dengan sejumlah asumsi (23 definisi, lima pengertian umum, dan lima postulat) dan berusaha untuk membuktikan semua hasil lain ( proposisi ) dalam pekerjaan. Yang paling terkenal dari postulat sering disebut sebagai “Kelima Postulat Euclid,” atau cukup dengan ” paralel mendalilkan “, yang dalam formulasi asli Euclid adalah:
Jika garis lurus jatuh pada dua garis lurus sedemikian rupa sehingga sudut interior pada sisi yang sama bersama-sama kurang dari dua sudut yang tepat, maka garis-garis lurus, jika diproduksi tanpa batas waktu, bertemu di sisi itu yang adalah sudut kurang dari dua kanan sudut.
Lain yang hebat matematika telah menemukan bentuk-bentuk sederhana dari properti ini (lihat postulat paralel untuk laporan setara). Terlepas dari bentuk dalil, bagaimanapun, secara konsisten tampaknya lebih rumit dari yang lain Euclid postulat (termasuk, misalnya, “Antara dua titik garis lurus bisa diambil”).
Setidaknya seribu tahun, geometers merasa kesulitan akibat kompleksitas yang berbeda dari kelima postulat, dan percaya itu bisa dibuktikan sebagai teorema dari keempat lainnya. Banyak berusaha untuk menemukan bukti oleh kontradiksi , termasuk matematikawan Arab Ibn al-Haytham (Alhazen, abad ke-11), dengan Persia matematikawan Umar Khayyām (abad 12) dan Nasir al-Din al-Tusi (abad ke-13), dan dengan Italia matematika Giovanni Girolamo Saccheri (abad 18).
Teorema Ibn al-Haytham, Khayyam dan al-Tusi pada segiempat , termasuk segiempat Lambert dan Saccheri segiempat , adalah “teorema pertama dari hiperbolik dan geometri berbentuk bulat panjang . ” Teorema-teorema bersama dengan alternatif mereka mendalilkan, seperti aksioma Playfair ‘s , memainkan peran penting dalam perkembangan selanjutnya dari non-Euclidean geometri. Upaya-upaya awal pada menantang kelima postulat memiliki pengaruh yang besar terhadap pembangunan di antara geometers kemudian Eropa, termasuk Witelo , Levi ben Gerson , Alfonso , John Wallis dan Saccheri. Semua upaya awal dibuat di mencoba untuk merumuskan non-Euclidean Namun geometri diberikan bukti cacat dari paralel mendalilkan, mengandung asumsi yang pada dasarnya setara dengan postulat paralel. Upaya-upaya awal itu, bagaimanapun, memberikan beberapa sifat awal dari geometri hiperbolik dan eliptik.
Khayyam, misalnya, mencoba untuk mendapatkan dari setara mendalilkan ia merumuskan dari “prinsip-prinsip Bertuah” ( Aristoteles ): “Dua garis lurus berpotongan konvergen dan tidak mungkin untuk dua garis lurus konvergen menyimpang ke arah di mana mereka bertemu. ” Khayyam kemudian dianggap sebagai tiga kasus yang tepat, tumpul, dan akut yang sudut puncak dari sebuah segiempat Saccheri dapat mengambil dan setelah membuktikan sejumlah teorema tentang mereka, ia benar membantah kasus tumpul dan akut berdasarkan dalil nya dan karena berasal klasik postulat Euclid yang tidak disadarinya adalah setara dengan postulat sendiri. Contoh lain adalah anak al-Tusi, Sadr al-Din (kadang-kadang dikenal sebagai “Pseudo-Tusi”), yang menulis sebuah buku tentang subjek di 1298, berdasarkan pengalaman kemudian al-Tusi, yang disajikan lain setara hipotesis untuk paralel dalil . “Dia pada dasarnya revisi kedua sistem Euclidean aksioma dan dalil-dalil dan bukti-bukti proposisi banyak dari Elemen.” Karyanya diterbitkan di Roma tahun 1594 dan dipelajari oleh geometers Eropa, termasuk Saccheri yang mengkritik pekerjaan ini serta yang dari Wallis.
Giordano Vitale , dalam bukunya Euclide restituo (1680, 1686), menggunakan Saccheri segiempat untuk membuktikan bahwa jika tiga poin adalah jarak yang sama di pangkalan AB dan CD KTT, maka AB dan CD di mana-mana berjarak sama.
Dalam sebuah karya berjudul Euclides ab Omni Naevo Vindicatus (Euclid Dibebaskan dari Semua Cacat), yang diterbitkan tahun 1733, Saccheri geometri eliptik cepat dibuang sebagai kemungkinan (beberapa orang lain dari aksioma Euclid harus dimodifikasi untuk geometri berbentuk bulat panjang untuk bekerja) dan mulai bekerja membuktikan besar jumlah hasil dalam geometri hiperbolik. Dia akhirnya mencapai titik di mana ia percaya bahwa hasil menunjukkan ketidakmungkinan geometri hiperbolik. Klaimnya tampaknya telah didasarkan pada pengandaian Euclidean, karena tidak ada kontradiksi logis hadir. Dalam upaya untuk membuktikan geometri Euclidean ia malah tidak sengaja menemukan sebuah geometri baru yang layak, tapi tidak menyadarinya.
Pada 1766 Johann Lambert menulis, tetapi tidak mempublikasikan, Theorie der Parallellinien di mana ia mencoba, sebagai Saccheri lakukan, untuk membuktikan postulat kelima. Dia bekerja dengan angka yang hari ini kita sebut segiempat Lambert, suatu segiempat dengan tiga sudut kanan (dapat dianggap setengah dari segiempat Saccheri). Dia segera menghilangkan kemungkinan bahwa sudut keempat adalah tumpul, karena memiliki Saccheri dan Khayyam, dan kemudian melanjutkan untuk membuktikan teorema banyak berdasarkan asumsi sudut akut. Tidak seperti Saccheri, ia tidak pernah merasa bahwa ia telah mencapai kontradiksi dengan asumsi ini. Dia telah membuktikan hasil non-Euclidean bahwa jumlah sudut dalam segitiga meningkat sebagai luas segitiga berkurang, dan ini menyebabkan dia untuk berspekulasi mengenai kemungkinan model kasus akut pada bola berjari-jari imajiner. Dia tidak membawa ide ini lebih jauh.
Pada saat ini itu sangat percaya bahwa alam semesta bekerja menurut prinsip-prinsip geometri Euclidean.
Penciptaan non-Euclidean geometri
Awal abad ke-19 akhirnya akan menyaksikan langkah-langkah yang menentukan dalam penciptaan non-Euclidean geometri. Sekitar 1830, Hungaria matematika János Bolyai dan Rusia matematika Nikolai Lobachevsky secara terpisah diterbitkan risalah pada geometri hiperbolik. Akibatnya, geometri hiperbolik disebut Bolyai-Lobachevskian geometri, baik sebagai matematikawan, independen satu sama lain, adalah penulis dasar non-Euclidean geometri. Gauss disebutkan kepada ayah Bolyai, ketika ditampilkan karya Bolyai muda, bahwa ia telah dikembangkan seperti geometri sekitar 20 tahun sebelumnya, meskipun ia tidak mempublikasikan. Sementara Lobachevsky menciptakan geometri non-Euclidean dengan meniadakan paralel mendalilkan, Bolyai bekerja di luar geometri di mana kedua Euclidean dan geometri hiperbolik yang mungkin tergantung pada k parameter. Bolyai berakhir karyanya dengan menyebutkan bahwa tidak mungkin untuk memutuskan melalui penalaran matematis saja jika geometri alam semesta fisik Euclid atau non-Euclidean, ini adalah tugas untuk ilmu fisik.
Bernhard Riemann , dalam sebuah kuliah yang terkenal pada 1854, mendirikan bidang geometri Riemann , membahas khususnya ide-ide sekarang disebut manifold , Riemannian metrik , dan kelengkungan . Ia dibangun sebuah keluarga tak terbatas geometri yang tidak Euclidean dengan memberikan rumus untuk keluarga metrik Riemann pada bola unit dalam ruang Euclidean . Yang paling sederhana ini disebut geometri berbentuk bulat panjang dan dianggap menjadi geometri non-Euclidean karena kurangnya garis paralel.
Terminologi
Itu Gauss yang menciptakan istilah “non-euclidean geometri”. Dia merujuk pada karyanya sendiri yang hari ini kita sebut geometri hiperbolik. Beberapa penulis modern yang masih menganggap “non-euclidean geometri” dan “geometri hiperbolik” menjadi sinonim. Pada tahun 1871, Felix Klein , dengan mengadaptasi metrik dibahas oleh Arthur Cayley pada tahun 1852, mampu membawa sifat metrik menjadi sebuah lokasi yang proyektif dan karena itu mampu menyatukan perawatan geometri hiperbolik, euclidean dan berbentuk bulat panjang di bawah payung projective geometri . Klein bertanggung jawab untuk istilah “hiperbolik” dan “eliptik” (dalam sistem, ia disebut geometri Euclidean “parabola”, sebuah istilah yang belum selamat dari ujian waktu). Pengaruhnya telah menyebabkan penggunaan saat ini dari “geometri non-euclidean” untuk berarti baik geometri “hiperbolik” atau “berbentuk bulat panjang”.
Ada beberapa hebat matematika yang akan memperpanjang daftar geometri yang harus disebut “non-euclidean” dengan berbagai cara. Dalam disiplin ilmu lainnya, terutama yang paling matematika fisika , istilah “non-euclidean” sering diartikan tidak Euclidean .
aksioma dasar non-Euclidean geometri
Geometri Euclidean aksiomatik dapat dijelaskan dalam beberapa cara. Sayangnya, sistem yang asli Euclid lima postulat (aksioma) bukan salah satu dari ini sebagai bukti nya mengandalkan asumsi tak tertulis beberapa yang juga seharusnya diambil sebagai aksioma. sistem Hilbert yang terdiri dari 20 aksioma paling dekat mengikuti pendekatan Euclid dan memberikan pembenaran untuk semua bukti Euclid. Sistem lain, menggunakan set yang berbeda dari istilah terdefinisi mendapatkan geometri yang sama dengan jalan yang berbeda. Dalam semua pendekatan, bagaimanapun, ada aksioma yang secara logis setara dengan kelima Euclid postulat, paralel dalil. Hilbert menggunakan bentuk aksioma Playfair, sementara Birkhoff , misalnya, menggunakan aksioma yang mengatakan bahwa “tidak ada sepasang yang sama tetapi tidak kongruen segitiga. ” Dalam salah satu sistem, penghapusan satu aksioma yang setara dengan postulat sejajar, dalam bentuk apapun yang diperlukan, dan meninggalkan semua aksioma lainnya utuh, menghasilkan geometri absolut . Sebagai pertama 28 proposisi Euclid (dalam The Elements) tidak memerlukan penggunaan postulat paralel atau apa setara dengan itu, mereka semua pernyataan benar dalam geometri mutlak.
Untuk mendapatkan geometri non-Euclidean, paralel dalil (atau ekuivalen) harus diganti oleh yang negasi . Meniadakan aksioma Playfair ‘s bentuk, karena itu adalah pernyataan majemuk (… terdapat satu dan hanya satu …), bisa dilakukan dengan dua cara. Entah ada akan ada lebih dari satu baris melalui paralel titik ke garis diberikan atau akan ada tidak ada garis melalui titik paralel ke garis yang diberikan. Dalam kasus pertama, menggantikan paralel dalil (atau ekuivalen) dengan pernyataan “Di pesawat, diberi titik P dan garis l tidak melewati P, terdapat dua garis melalui P yang tidak memenuhi l” dan menjaga semua aksioma lainnya, hasil geometri hiperbolik . Kasus kedua tidak ditangani dengan mudah. Cukup mengganti paralel mendalilkan dengan pernyataan, “Dalam pesawat, diberi titik P dan garis l tidak melewati P, semua garis melalui P memenuhi l”, tidak memberikan satu set konsisten aksioma. Ini mengikuti sejak garis paralel ada di geometri mutlak , tetapi pernyataan ini mengatakan bahwa tidak ada garis paralel. Masalah ini dikenal (dalam kedok yang berbeda) untuk Khayyam, Saccheri dan Lambert dan merupakan dasar untuk menolak mereka apa yang dikenal sebagai “kasus sudut tumpul”. Untuk mendapatkan satu set konsisten aksioma yang meliputi aksioma ini tentang tidak memiliki garis paralel, beberapa aksioma lain harus tweak. Penyesuaian harus dibuat tergantung pada sistem aksioma yang digunakan. Beberapa diantaranya tweak akan memiliki efek memodifikasi kedua postulat Euclid dari pernyataan bahwa segmen garis dapat diperpanjang tanpa batas waktu untuk pernyataan bahwa garis tak terbatas. Riemann ‘s geometri eliptik muncul sebagai geometri paling alami memuaskan aksioma ini.
Model non-Euclidean geometri
 Untuk rincian lebih lanjut tentang topik ini, lihat Model non-Euclidean geometri .
Untuk rincian lebih lanjut tentang topik ini, lihat Model non-Euclidean geometri .
Pada bola, jumlah sudut segitiga tidak sama dengan 180 °. Permukaan sebuah bola bukan ruang Euclidean, tetapi secara lokal hukum geometri Euclidean adalah perkiraan yang baik. Dalam sebuah segitiga kecil di muka bumi, jumlah dari sudut sangat hampir 180 °.
Dua geometri Euclidean dimensi dimodelkan dengan gagasan kita tentang “datar pesawat . “
geometri Elliptic
Model sederhana untuk geometri eliptik adalah bola, di mana garis ” lingkaran besar “(seperti ekuator atau meridian di dunia ), dan poin yang berlawanan satu sama lain (disebut poin antipodal ) diidentifikasi (dianggap sama). Ini juga salah satu model standar dari pesawat proyektif nyata . Perbedaannya adalah bahwa sebagai model geometri eliptik metrik diperkenalkan memungkinkan pengukuran panjang dan sudut, sedangkan pada model pesawat proyektif tidak ada metrik tersebut.
Dalam model berbentuk bulat panjang, untuk setiap garis yang diketahui ℓ dan titik A, yang tidak pada ℓ, semua baris melalui A akan berpotongan ℓ.
geometri hiperbolik
Bahkan setelah pekerjaan Lobachevsky, Gauss, dan Bolyai, pertanyaannya tetap: apakah model seperti itu ada untuk geometri hiperbolik ? Model untuk geometri hiperbolik dijawab oleh Eugenio Beltrami , pada 1868, yang pertama kali menunjukkan bahwa permukaan yang disebut pseudosphere memiliki sesuai kelengkungan untuk model sebagian dari ruang hiperbolik , dan dalam makalah kedua di tahun yang sama, mendefinisikan Model Klein yang model keseluruhan dari ruang hiperbolik, dan digunakan ini untuk menunjukkan bahwa geometri Euclidean dan geometri hiperbolik adalah equiconsistent , sehingga geometri hiperbolik adalah logis konsisten jika dan hanya jika geometri Euclidean adalah. (Implikasi terbalik berikut dari horosphere model geometri Euclidean.)
Dalam model hiperbolik, dalam bidang dua dimensi, untuk setiap garis yang diketahui ℓ dan Titik, yang tidak pada ℓ, ada tak terhingga banyak baris melalui A yang tidak berpotongan ℓ.
Dalam model ini konsep-konsep non-Euclidean geometri sedang diwakili oleh objek Euclidean dalam pengaturan Euclidean. Ini memperkenalkan sebuah distorsi perseptual dimana garis-garis lurus dari geometri non-Euclidean yang diwakili oleh kurva Euclidean yang secara visual membungkuk. Ini “lentur” bukan milik non-Euclidean baris, hanya kecerdasan dari cara mereka diwakili.
sifat Jarang
Euclid dan geometri non-Euclidean secara alami memiliki sifat serupa, yaitu mereka yang tidak tergantung pada sifat paralelisme. Kesamaan ini adalah subjek dari geometri netral (juga disebut geometri absolut). Namun, sifat yang membedakan satu geometri dari yang lain adalah orang-orang yang secara historis menerima perhatian yang besar.
Selain perilaku baris sehubungan dengan tegak lurus umum, disebutkan dalam pendahuluan, kami juga memiliki berikut ini:
- Sebuah segiempat Lambert adalah segiempat yang memiliki tiga sudut kanan. Sudut keempat dari segiempat Lambert adalah akut jika geometri hiperbolik, sebuah sudut yang tepat jika geometri Euclidean adalah atau tumpul jika geometri adalah berbentuk bulat panjang. Akibatnya, empat persegi panjang hanya ada dalam geometri Euclidean.
- Sebuah segiempat Saccheri adalah segiempat yang memiliki dua sisi dengan panjang yang sama, baik tegak lurus ke samping disebut basis. Dua lainnya dari sudut segiempat Saccheri disebut sudut puncak dan mereka memiliki ukuran yang sama. Sudut puncak dari sebuah segiempat Saccheri yang akut jika geometri hiperbolik, sudut yang tepat jika geometri Euclidean adalah sudut tumpul dan jika geometri adalah berbentuk bulat panjang.
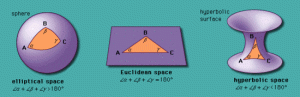
- Jumlah dari ukuran sudut segitiga apapun adalah kurang dari 180 ° jika geometri hiperbolik, sama dengan 180 ° jika geometri Euclidean, dan lebih besar dari 180 ° jika geometri adalah berbentuk bulat panjang. Cacat segitiga adalah nilai numerik (180 ° – jumlah dari ukuran sudut segitiga). Hasil ini juga dapat dinyatakan sebagai: cacat segitiga dalam geometri hiperbolik adalah positif, cacat segitiga dalam geometri Euclidean adalah nol, dan cacat segitiga dalam geometri eliptik adalah negatif.
Pentingnya
Non-Euclidean geometri adalah contoh dari sebuah pergeseran paradigma dalam sejarah ilmu pengetahuan . Sebelum model pesawat non-Euclidean yang disajikan oleh Beltrami, Klein, dan Poincaré, geometri Euclidean berdiri tertandingi sebagai model matematika dari ruang . Selain itu, karena substansi subjek dalam geometri sintetis adalah pameran kepala rasionalitas, titik Euclidean pandang diwakili otoritas mutlak. Non-Euclidean geometri, meskipun diasimilasi oleh peneliti dipelajari, terus menjadi tersangka bagi mereka yang tidak memiliki paparan konsep hiperbolis dan elips.
Penemuan non-Euclidean geometri memiliki efek riak yang jauh melampaui batas-batas matematika dan ilmu pengetahuan. Filsuf Immanuel Kant pengobatan itu pengetahuan manusia memiliki peran khusus untuk geometri. Itu adalah contoh utama tentang sintetis pengetahuan apriori, tidak berasal dari indera atau disimpulkan melalui logika – pengetahuan kita tentang ruang merupakan kebenaran bahwa kita dilahirkan dengan. Sayangnya bagi Kant, konsepnya ini geometri unalterably benar adalah Euclidean. Teologi juga dipengaruhi oleh perubahan dari kebenaran absolut untuk kebenaran relatif dalam matematika yang adalah hasil dari pergeseran paradigma.
Keberadaan non-Euclidean geometri berdampak pada “kehidupan intelektual” dari Inggris Victoria dalam banyak hal dan khususnya adalah salah satu faktor yang menyebabkan yang menyebabkan pemeriksaan ulang pengajaran geometri berdasarkan Euclid ‘s Elemen . Masalah kurikulum yang hangat diperdebatkan pada saat itu dan bahkan subyek dari bermain, Euclid dan Rivals modern, ditulis oleh penulis Alice in Wonderland .
nguồn